Medida

A classe central do LabIFSC2 é a Medida, tecnicamente ela representa uma variável aleatória gaussiana, portanto, é necessário fornecer uma média $\mu$ e um desvio padrão $\sigma$, além disso, é possível oferecer uma unidade e realizar conversões de unidade. A forma como um objeto dessa classe é printado obedece convenções de notação científica que podem ser alteradas

Propagação de Erros

Toda a propagação de erros é implementada usando uma simulação Monte Carlo, em casos de solução analítica simples é implementada a propagação exata

Operações básicas

    import LabIFSC2 as lab
    x=lab.Medida(4,0.1)
    y=lab.Medida(0.4,0.05)
    #Operações básicas
    print(x+y)#(4.40 ± 0.10) 
    print(x-y)#(3.60 ± 0.10) 
    print(x*y)#(1.60 ± 0.20) 
    print(x/y)#(1.0 ± 0.1)E1 
    #Exponenciação
    print(x**y)#(1.75 ± 0.10) 
    print(x**2)#(16 ± 1)
    print(3**x)#(81 ± 1)

Valor nominal e incerteza

Cada instância da classe Medida possui atributos associados a média e o desvio padrão, caso não seja especificado unidades, os atributos SI serão iguais aos originais

Valor nominal e incerteza de uma medida

    import LabIFSC2 as lab
    x=lab.Medida(156,2,'cm')
    print(x.nominal)#156
    print(x.si_nominal)#1.56
    print(x.incerteza)#2
    print(x.si_incerteza)#0.02

Igualdade entre Medidas

A igualdade ou diferença entre Medidas só pode ser determinada uma vez que as Medidas tenham dimensões compativeis, caso contrário, será retornado um erro pela função checa_dimensao. Foi definido que duas Medidas são iguais se $|(\mu_1 - \mu_2)| \le 2(\sigma_1 + \sigma_2$) e são diferentes caso $|(\mu_1 - \mu_2)| \le 3(\sigma_1 + \sigma_2$), o caso que a diferença entre os valores nominais estiverem entre duas e três vezes a soma das incertezas é considerado inconclusivo e é retornado None

Histograma

Tecnicamente, algumas operações da biblioteca geram variáveis não gaussianas, um exemplo seria a divisão entre duas medidas $z=x/y$, nesse caso, o histograma com a distribuição de probabilidade é armazenado em um atributo chamado histograma

Histograma de uma medida

    import LabIFSC2 as lab
    z=lab.Medida(5,0.5)/lab.Medida(43,10)
    print(z) # (0.12±0.04)
    print(z.histograma) #array([0.1329215 , 
    #0.17917796, 0.10256415, ..., 0.11928206])

Usando a função hist do Matplotlib é possível visualizar esse histograma

Plotando histograma

    import matplotlib.pyplot as plt
    plt.hist(z.histograma,bins=100)
    plt.savefig('exemplo de histograma.jpg')

A distribuição é visivelmente não gaussiana, por isso é necessário armazena-la nesse atributo de forma que os cálculos de propagação de erro sejam precisos

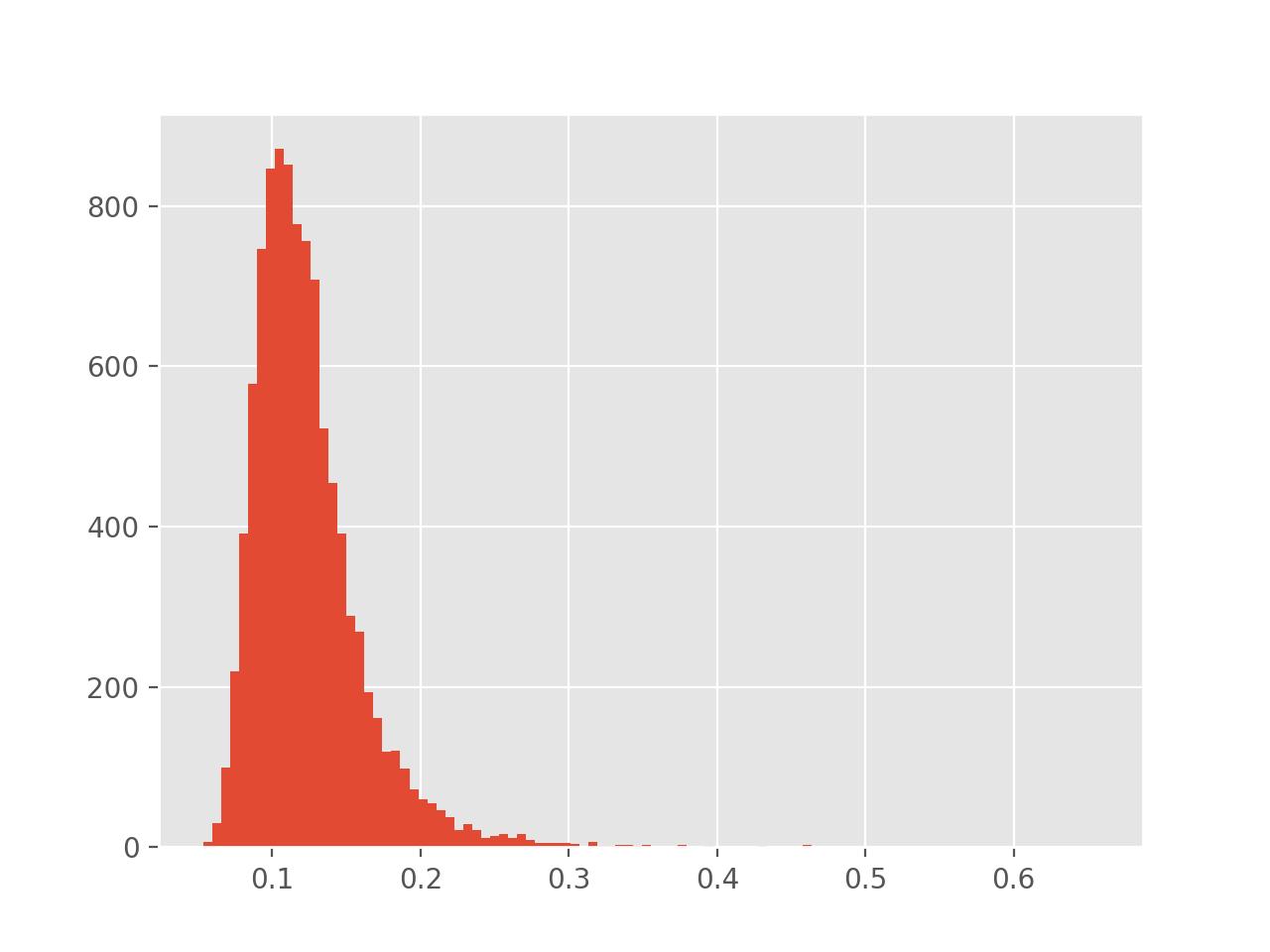
Probabilidade

Como cada instância da classe Medida possui um atributo de histograma é interessante responder a pergunta, qual é a chance de minha Medida estar entre $[a,b]$? A classe Medida possui um método chamado probabilidade que recebe um começo $a$ e um final $b$ e retorna a probabilidade

Probabilidade de uma Medida

    import LabIFSC2 as lab
    print(lab.Medida(5,0.1).probabilidade(4.9,5.1)) #0.6878
    print(lab.Medida(5,0.1).probabilidade(4.8,5.2)) #0.952
    print(lab.Medida(5,0.1).probabilidade(4.7,5.3)) #0.9973

    z=lab.Medida(5,0.1)**3
    print(z.probabilidade(110,130)) #0.7291

Retorna a probabilidade que a Medida esteja entre [a,b] usando o histograma como referencia

Parameters:

Name	Type	Description	Default
a	float	Extremo inferior	required
b	float	Extremo superior	required

Returns:

Name	Type	Description
probabilidade	float	(float) probabilidade de estar entre [a,b]

Source code in LabIFSC2/medida.py

def probabilidade(m,a,b) -> float:
    ''' Retorna a probabilidade que a Medida
    esteja entre [a,b] usando o histograma como
    referencia

    Args:
        a (float): Extremo inferior
        b (float): Extremo superior

    Returns:
        probabilidade: (float) probabilidade de estar entre [a,b]

    '''

    if not len(m.histograma):
        m.histograma=np.random.normal(m.nominal,
                    m.incerteza,10_000)
    condition=np.logical_and(m.histograma>=a,m.histograma<=b)
    chance=np.count_nonzero(condition)/len(m.histograma)
    return chance

Compatibilidade com o LabIFSC original

O método tradicional usado no LabIFSC é uma propagação de erros lineares, é usada uma expansão de Taylor com centro em $\mu$. No caso que os erros forem pequenos em comparação a variação da função tanto o LabIFSC quanto o LabIFSC2 chegaram em resultados equivalentes, testes unitários exatamente sobre isso podem ser encontrados no repositório, eis um exemplo:

Source code in tests/test_lab1vslab2.py

def test_funcoes_matematicas():
    nominais=np.random.random(100)
    incertezas=np.random.random(100)/100
    for nominal,incerteza in zip(nominais,incertezas):
        x=lab1.sin(lab1.Medida((nominal,incerteza)))
        y=lab2.sin(lab2.Medida(nominal,incerteza))
        assert igualdade_medida(x,y)
        x=lab1.cos(lab1.Medida((nominal,incerteza)))
        y=lab2.cos(lab2.Medida(nominal,incerteza))
        assert igualdade_medida(x,y)